arisa19811020

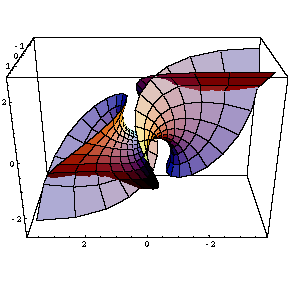
luna[u_,v_]:={ u - u^5 /5 + 2 u^3 v^2 - u v^4,-v - u^4 v + 2 u^2 v^3 - v^5 /5, 2 u^3 /3-2 u v^2}

gr=ParametricPlot3D[Evaluate[luna[u,v]],{u,-1.25,1.25},{v,-1.25,1.25}]

Show[{gr},ViewPoint->{0,2,1}]

特徴：

第１基本量 E=(1+u^4+2u^2v^2+v^4)^2, F=0, G=(1+u^4+2u^2v^2+v^4)^2,

第２基本量 L=-4u,　　M=4v,　　N=4u

ガウス曲率 K=-16(u^2+v^2)/(1+u^4+2u^2v^2+v^4)^4

平均曲率 H=0

法写像は球の３分の２を覆うように動く。 正しくないような気がするけれど、このようにかいたのは、集 中講義のホームページ（２．曲面の基本量を計算する）を利用 して単位法ベクトル場がどのくらいの範囲を動いたかというと ころの図形をみて、そのように表現した。

曲面は横から見たら気が付かなかったが、 真上（｛0,0,1｝）から見るとトンネルのような形があって驚いた。

rats_suger1113

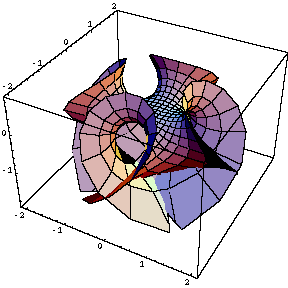
trumprt[u_,v_] :={ u-1/7*u^7+3*u^5*v^2-5*u^3*v^4+u*v^6, -v-u^6*v+5*u^4*v^3-3*u^2*v^5+1/7*v^7, 1/2*u^4-3*u^2*v^2+1/2*v^4}

gr=ParametricPlot3D[Evaluate[trumprt[u,v]],{u,-1.15,1.15},{v,-1.15,1.15}]

特徴： 全体として丸みをおびていて、コンパクトにおさまって いるところです。-1.15,1.15の値を変えると、また違った曲面 になります。 （コンパクトというのは数学用語があるので この場面で使うには注意が必要ですし， 違った曲面というのも問題があります． でも面白い形が出てきましたね．）

Back to FURUHATA's Home Page