1.曲線,曲面の初等微分幾何

計算機室で Mathematica を立ち上げる. 以下にあるコマンドラインを打ち込むかカット・アンド・ペーストして, 実行する.実行はEnter キー(あるいはshift+return キー)でなされる.
パラメータ表示(媒介変数表示)されている3次元空間内の曲面は, ParametricPlot3D というグラフィック関数を用いて描くことができる.
たとえば,原点中心の半径1の2次元球面における球面極座標を思い出そう. 3次元空間の各座標 X,Y,Z がパラメータ u,v の関数として,
{Cos[u] Cos[v], Cos[u] Sin[v], Sin[u] }
と表す.u の範囲が -Pi/2 から Pi/2 まで,v の範囲が -Pi から Pi まで考えて,このパラメータ表示が 表す図形を図示してみる:
ParametricPlot3D[
{Cos[u] Cos[v], Cos[u] Sin[v], Sin[u] },
{u, -Pi/2, Pi/2}, {v, -Pi, Pi},
Ticks -> None,
PlotPoints -> 20,
ViewPoint -> {-1.0, 2.0, 3.0} ]
オプションにある PlotPoints -> 20 は,u,v の範囲をおのおの20等分せよ,という意味である (u の範囲を 10 等分,v の範囲を 15 等分したければ,PlotPoints -> {10,15} とする). ViewPoint は文字どおり眺める方向を意味する(メニュー input から 3D Viewpoint selector を選べば,簡単に方向を入力できる). その他,種々のオプションがある.
u の範囲を -1 から 1 までとすれば,北極と南極の回りが省かれる:
ParametricPlot3D[
{Cos[u] Cos[v], Cos[u] Sin[v], Sin[u] },
{u, -1,1}, {v, -Pi, Pi},
Ticks -> None,
PlotPoints -> 20,
ViewPoint -> {-1.0, 2.0, 3.0} ]
さて, 方程式で表された曲面の図示は,一般には大変困難なのである(特異点の処理が大変). したがって,ふつうどうするかというえば, 方程式を満たすようにうまいパラメータ表示を見い出してから,上記のような関数 ParametricPlot3D 等を用いる.
まず、楕円面。これは X^2/(a^2) + Y^2/(b^2) + Z^2 /(c^2) = 1 で表される曲面である。パラメータ表示は
ellipsoid[a_,b_,c_][u_,v_]:={a Cos[u] Cos[v], b Cos[u] Sin[v], c Sin[u] };
で与えることができる( u,v がパラメータで,上の3つの関数が X,Y,Z 座標に対応している). 例として, a=1, b=2, c=3 の場合を考えよう.Mathematica でこの曲面を描かせると, 以下のようになる。
(* ellipsoid *)
ParametricPlot3D[
ellipsoid[1,2,3][u,v],
{u, -Pi/2, Pi/2}, {v, -Pi, Pi},
Ticks -> None, PlotRange -> {-3, 3},
PlotPoints -> 20,
ViewPoint -> {-1.0, 2.0, 3.0} ]
双曲面には1葉双曲面と2葉双曲面がある。1葉双曲面は X^2/(a^2) + Y^2/(b^2) - Z^2 /(c^2) = 1 が標準形である。 パラメータ表示は,双曲三角関数と三角関数を用いて
hyperboloid[a_,b_,c_][u_,v_]:= { a Cosh[u] Cos[v], b Cosh[u] Sin[v], c Sinh[u] };
で与えることができる. a=1, b=1, c=1 の場合を図示してみよう.
(* hyperboloid of one sheet*)
ParametricPlot3D[
hyperboloid[1,1,1][u,v],
{u, -1, 1}, {v, -Pi, Pi},
Ticks -> None, PlotRange -> {-3, 3},
PlotPoints -> 20, Axes -> None,
ViewPoint -> {-1.0, 2.0, 4.0} ]
1葉双曲面は、その各点で、その点を通りこの曲面上に乗っている直線がちょうど2本存在する。
とくに,
a=b のとき,1葉双曲面は,
Z 軸とねじれの位置にある直線を Z 軸回りに回転して得られる回転面であることもわかるであろう。
(*Hyperboloid of one sheet
as a ruled surface*)
ParametricPlot3D[
{ Cos[u] - v Sin[u], Sin[u] + v Cos[u], v },
{u, -Pi, Pi}, {v, -1, 1},
Ticks -> None, PlotRange -> {-3, 3},
PlotPoints -> 20, Axes -> None,
ViewPoint -> {-1.0, 2.0, 4.0} ]
2葉双曲面は - X^2/(a^2) - Y^2/(b^2) + Z^2 /(c^2) = 1 が標準形である。2つの連結成分が存在する。 Z=0 (xy-座標平面)に関して,上部にある連結成分と下部にある成分がある. 片方の成分のパラメータ表示は,
hyperboloid2[a_,b_,c_][u_,v_]:={ a Sinh[u] Cos[v], b Sinh[u] Sin[v], c Cosh[u] } ;
hyperboloid2m[a_,b_,c_][u_,v_]:={ a Sinh[u] Cos[v], b Sinh[u] Sin[v], -c Cosh[u] };
で与えられる.もう片方は,Z 成分を -1 倍すればよい. a=1, b=2, c=3 の場合を図示しよう。
(* hyperboloid *)
S1:=ParametricPlot3D[
hyperboloid2[1,2,3][u,v],
{u, -2, 2}, {v, -Pi, Pi},
Ticks -> None,
PlotPoints -> 15, Axes -> None,
ViewPoint -> {-1.0, 1.2, 1.5} ];
S2:=ParametricPlot3D[
hyperboloid2m[1,2,3][u,v],
{u, -2, 2}, {v, -Pi, Pi},
Ticks -> None,
PlotPoints -> 15, Axes -> None,
ViewPoint -> {-1.0, 1.2, 1.5} ];
Show[S1,S2]
先に書いた双曲面の標準形の右辺の値1を変数 d で置き換えると、
X^2/(a^2) + Y^2/(b^2) - Z^2 /(c^2) = d
d > 0 の場合は1葉双曲面で、d < 0 の場合は2葉双曲面である。 その境目となる d=0 の場合が、2次錐面である。
(* quadratic cone *)
ParametricPlot3D[
{ u Cos[v], 2 u Sin[v], 3 u },
{u, -2, 2}, {v, -Pi, Pi},
Ticks -> None, AspectRatio -> 1,
PlotPoints -> 15, Axes -> None,
ViewPoint -> {-1.0, 1.0, 1.2} ]
楕円的方物面は X^2/(a^2) + Y^2/(b^2) =c^2 Z が標準形で、 以下のパラメータ表示であらわすことができる.
paraboloid[a_,b_,c_][u_,v_]:={ a u Cos[v], b u Sin[v], (1/c)^2 u^2 }
a=1, b=1,c=1 の場合,図示してみると,
(* Elliptic paraboloid *)
ParametricPlot3D[
paraboloid[1,1,1][u,v],
{u, -5, 5}, {v, -Pi, Pi},
Ticks -> None,
PlotPoints -> 15, Axes -> None,
ViewPoint -> {-1.0, 1.0, 1.2} ]
ParametricPlot3D よりも、関数 Z=f(X,Y)= 1/c^2 ( X^2/(a^2) + Y^2/(b^2) ) のグラフとして表した方がわかりやすいであろう。 2変数関数のグラフを描くには Plot3D を用いる。
(* Elliptic paraboloid *)
Plot3D[ x^2 / 2 + y^2 / 4, {x, -1, 1}, {y, -1, 1},
Ticks -> None, AspectRatio -> 1,
PlotPoints -> 15, Axes -> None,
ViewPoint -> {1.0, 1.2, 0.6} ]
双曲的方物面は X^2/(a^2) - Y^2/(b^2) =c^2 Z が標準形で、 これも Plot3D を用いてみてみよう(a=1, b=1, c=1 の場合)。
(* Hyperbolic paraboloid *)
Plot3D[ x^2 - y^2,
{x, -1, 1}, {y, -2, 2},
Ticks -> None, AspectRatio -> 1,
PlotPoints -> 15, Axes -> None,
ViewPoint -> {1.0, 1.2, 0.6} ]
まず針金でできた同じ大きさの円を平行にしてその2つの円を境界とするようなシャボン膜をつくると、それはカテノイドと呼ばれる曲面となる。これは平面曲線カテナリー
catenary[c_][t_]:={ c Cosh[t/c], t} ;
の回転面である。
(* Catenoid *)
ParametricPlot3D[
{ Cosh[u ] Cos[v], Cosh[u ] Sin[v], u },
{u, -1, 1}, {v, -Pi, Pi},
Ticks -> None, PlotRange -> {-1, 1},
Boxed -> False,
PlotPoints -> 15, Axes -> None,
ViewPoint -> {-1.0, 2.0, 2.2} ]
螺旋状に針金を巻き、これを境界とするシャボン膜をつくると、それはヘリコイド(螺旋面)とよばれる曲面となる。
(* helicoid *)
ParametricPlot3D[
{ v Cos[u], v Sin[u], u },
{u, -Pi, Pi},{v, -1, 1},
Ticks -> None, PlotRange -> {-3.2, 3.2},
Boxed -> False,
PlotPoints -> 30
, Axes -> None,
ViewPoint -> {-1.0, 2.0, 4.0} ]
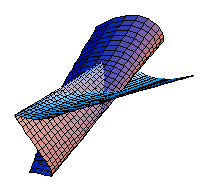
つぎは,自己交差を有する極小曲面の例である(エンネッパーの曲面と呼ばれる)。
(* Enneper surface *)
ParametricPlot3D[
{ u + u v^2- u^3/3, v + u^2 v - v^3 /3, u^2-v^2 },
{u, -2, 2}, {v, -2, 2},
Ticks -> None, PlotRange -> {-2.5, 4},
PlotPoints -> 30,
ViewPoint -> {-1.0, 2.0, 2.0} ]
以下であげる例は、空間曲線の接可展開面と呼ばれるものである。空間曲線が与えられたときにその曲線上の点の接線をすべて集めて得られてできる曲面である。ここでは、空間曲線の捩率がどこでも0でないものと0となる点を有する場合の2通りにおいて、もっとも簡単な例を挙げる。まず定義しておこう:
(* tangent developable of curves *)
Tangentdev[alpha_][u_, v_]:= alpha[uu] + v D[alpha[uu],uu] /. uu->u ;
Curve1[u_]:={u,u^2,u^3};
Curve2[u_]:={u,u^2,u^4};
はじめの例では空間曲線の捩率がどこでも0でない。ちなみに、常に 接可展開面は、もとの空間曲線のところで特異点(写像の微分のランクが2でない点)となっている。
ParametricPlot3D[
Tangentdev[Curve1][u,v],
{u, -0.5, 0.5}, {v, -1, 1},
Ticks -> None, PlotRange -> {-1, 1},
Boxed -> False,
PlotPoints -> 10, Axes -> None,
ViewPoint -> {1.0, 1.0, 4.0} ]
次の例では、原点において、もとの空間曲線の捩率が0となる。この場合、接可展開面は、少し複雑な形となる。いろいろと角度を変えて眺めてみよう。
ParametricPlot3D[
Tangentdev[Curve2][u,v],
{u, -0.5, 0.5}, {v, -1, 1},
Ticks -> None, PlotRange -> {-1, 1},
Boxed -> False,
PlotPoints -> 10, Axes -> None,
ViewPoint -> {1.0, 1.0, 4.0} ]
ここで扱う平面曲線は,パラメータ付けられた滑らかな曲線を意味することにします. 実数の区間 [a,b] (もしくは円周)から平面 R^2 への滑らかな写像 (無限回連続微分可能な2次元ベクトル値関数)のことです (実は以下の議論では,C^3 級,すなわち3階の導関数まで存在してそれらが連続関数になっているもの, という仮定だけで十分です). まず,各自のフロントエンドで立ち上げている Mathematica のノートブックに, つぎを書いて Enter を押しましょう.
alpha[t_]:={a1[t],a2[t]};
J[{p1_,p2_}]:={-p2,p1};
2行目は,平面ベクトルを反時計回りに90度回転させる,という作用素 J を定義しています (平面上の点 {x, y} を複素数 x + sqrt[-1] y と考えれば,作用素 J は sqrt[-1] を掛ける操作である).
次に,平面曲線 alpha の曲率を表す Mathematica 上の関数を定義しましょう. 平面曲線 alpha を引数にもつ t の関数 kappa2[alpha_] を次で定義します.
(* curvature *)
kappa2[alpha_][t_]:=
D[alpha[tt],{tt,2}].J[D[alpha[tt],tt]]/Simplify[D[alpha[tt],tt].D[alpha[tt],tt]]^(3/2)/. tt->t ;
D[alpha[tt],tt]] と D[alpha[tt],{tt,2}] は,点 tt における1階と2階の微分を表す Mathematica の記号です. ここでは,おのおの alphaの速度ベクトルおよび加速度ベクトルを意味します.
時刻 t に於ける alphaの速度ベクトルの大きさ(ノルム)を,t の関数として 次のように名前をつけておきましょう.
(* norm of velocity vectors *)
arclengthprime[alpha_][t_]:=
Sqrt[Simplify[D[alpha[tt],tt].
D[alpha[tt],tt]]]/. tt->t ;
関数arclengthprime[alpha_]の不定積分と,t=a から t=b までの定積分を次の記号で表すことにします. 前者は alphaの弧長パラメータ s(t) であり,後者は t=a から t=b までの曲線の長さです. 3つ目のものは,数値積分(NIntegrate)を行わせるものです.
(* Arclength *)
arclength[alpha_][t_]:=
Integrate[arclengthprime[alpha][tt],tt]/. tt->t ;
length[a_,b_][alpha_]:=
Integrate[arclengthprime[alpha][u],{u,a,b}] ;
nlength[a_,b_][alpha_]:=
NIntegrate[arclengthprime[alpha][u],{u,a,b}] ;
次に,平面曲線 alphaの曲率中心の軌跡が表す平面曲線にevolute[alpha_]という名前を付けておきます. これは平面曲線alphaの縮閉線と呼ばれ,平面曲線alphaの法線族の包絡線になっています(つまり,縮閉線の各点の接線はalpha のある点での法線となっている).このことはあとで 確認することになるでしょう.
(* evolute of a curve --- curves produced by curvature centers *)
evolute[alpha_][t_]:=
alpha[tt]+D[alpha[tt],tt].D[alpha[tt],tt]/
(D[alpha[tt],{tt,2}].J[D[alpha[tt],tt]]) J[D[alpha[tt],tt]] /. tt->t ;
縮閉線とは反対に次のことを考えます.勝手な平面曲線は,常にある平面曲線の縮閉線となり得ます. 曲線 alpha を縮閉線とするような曲線は 曲線 alphaの伸開線と呼ばれます.これにinvolute[alpha_,a_]という名前をつけておきます.引数a_の意味は定義式の右辺を見れば分かるでしょう (図を描いてみれば,一目瞭然).
(* involute of a curve *)
involute[alpha_,a_][t_]:=
alpha[tt]+(a - arclength[alpha][tt]) D[alpha[tt],tt]/
Sqrt[Factor[D[alpha[tt],tt].D[alpha[tt],tt]]] /. tt->t ;
曲線alphaの時刻 t における点を始点として,速度ベクトルの方向に長さが s の線分を tangentline[alpha_][s_,t_] で表し, 速度ベクトルを反時計回りの90度回転させたベクトルの方向に長さが s の線分を normalline[alpha_][s_,t_] で表すことにします.s=1 にとれば,これは曲線のフレネー標構と呼ばれるものですね.
(* lines parallel to the Frenet frame *)
tangentline[alpha_][s_,t_]:=
Line[{alpha[tt],alpha[tt]+s D[alpha[tt],tt]/Sqrt[Factor[D[alpha[tt],tt].D[alpha[tt],tt]]]}] /. tt->t ;
normalline[alpha_][s_,t_]:=
Line[{alpha[tt],alpha[tt] + s J[D[alpha[tt],tt]]/(D[alpha[tt],tt].D[alpha[tt],tt])^(1/2)}] /. tt->t ;
ひとまず,上のようにして,新たに関数たちを Mathematica に覚えてもらったことになります (読み込ませる際に Enter を押しましたか?大丈夫ですね?). 以下で,これらの関数を使って,具体的な曲線に対して曲線の性質をみてみることにしよう.
(* Examples of plane curves (1) *)
ellipse[a_,b_][t_]:={a Cos[t], b Sin[t]};
limacon[a_,b_][t_]:=(2a Cos[t]+b){Cos[t], Sin[t]};
cardioid[a_][t_]:={2a Cos[t](1+Cos[t]), 2a Sin[t](1+Cos[t])} ;
curve3[a_,b_,c_,d_][t_]:={t, a t^3 + b t^2 + c t + d};
Enter Key を押して読み込ませましたか?
例えば,正弦関数のグラフを -2Pi から 2Pi まで見たいときは,"Plot" を使って
Plot[ Sin[t], {t, -2 Pi, 2Pi } ]
と入力して Enter key を押せば実行に移され,見慣れたグラフが簡単に描き出されます.
"ParametricPlot" を使って,別名「心臓形」と呼ばれるカージオイドの形を見てみましょう.
ParametricPlot[cardioid[1][t], {t,0,2Pi},AspectRatio->Automatic] ;
{t,0,2Pi} で変数 t が動く範囲を指定します.AspectRatio->Automatic は,図の縦横の比率の自動化というオプションです.AspectRatio->{1,1} とすれば,縦横の比率が1:1とすることを意味します.
ParametricPlot[
Evaluate[{ ellipse[1.5,1][t], evolute[ellipse[1.5,1]][t]} ],
{t,0,2Pi},AspectRatio->Automatic];
縮閉線がカスプ(尖点)が4つ現れているのがはっきり分かりますね.
これらの点では縮閉線の速度ベクトルが0になります.
一般に,平面曲線で速度ベクトルが0となる点をその平面曲線の特異点と呼びます.
この楕円の縮閉線には4つの特異点があります.
ellipse[1.5,1][t] の曲率のグラフも見てみましょう.
Plot[kappa2[ellipse[1.5,1]][t], {t,0,2Pi}]
この関数は周期関数(周期は2Pi)に注意すれば,極値が4つあることが分かりますね.
曲率の値がすべての点で正であることにも注意しましょう.
一般に,曲率の微分が0になる点をその平面曲線の頂点と呼びます.この楕円は4つの頂点を持っていることになります.
前に簡単な計算で示したように,曲率の値が 0 でないとき,
縮閉線の速度ベクトルが 0 になる ←→ もとの曲線の曲率の微分が0になる,
即ち,縮閉線の特異点 ←→ 平面曲線の頂点
です.つまり,楕円の縮閉線に現れる4つのカスプは楕円の4つの頂点に対応していることが分かります.
○ 楕円の長軸や短軸の長さを変えて同じことをしてみなさい.例えば,ellipse[3,1][t] , ellipse[1.2,1][t] , ... など.
楕円でなく円ではどうでしょうか.ellipse[a,b] のパラメータ a と b の値が等しいとき,これは半径 1 の円を表すのでした.
ParametricPlot[
Evaluate[{ ellipse[1.5,1][t], evolute[ellipse[1,1]][t]} ],
{t,0,2Pi},AspectRatio->Automatic];
明らかに,縮閉線は原点に停留することになります.曲率は値が 1 の定数関数となり,円上のすべての点が頂点となります.
●4.2 カージオイドcardioid[1][t](リマソン limacon[0.5,1][t] と同じであることに注意)について同じことを観察してみましょう.
ParametricPlot[
Evaluate[{ cardioid[1][t], evolute[cardioid[1]][t]} ],
{t,0,2Pi},AspectRatio->Automatic];
今度は,もともとの曲線のカージオイド自身に特異点--カスプがあります. 縮閉線にも1つのカスプが見えますね.カージオイドの曲率のグラフはどうなるでしょうか.
Plot[kappa2[cardioid[1]][t], {t,0,2 Pi}]
これも周期関数です. t=0 で極小値(値は正)を取っています.曲率のグラフは t=Pi 付近で急上昇していますが,これは t=Pi でカージオイドがカスプを持つことに拠ります. カスプ(t=Pi )では曲率は無限大に発散してしまい実数値として定義できません. 一方,曲率半径(曲率の逆数)は 0 に収束しますから, 曲率中心はカージオイドのカスプに収束することになります.ParametricPlot の図で, カージオイドとその縮閉線が,カージオイドのカスプの点で重なっているのが見て分かりますね. しかし,図では分からないのですが,縮閉線の方も t=Pi で特異点となります( t=Pi で速度ベクトルが 0 となる). これを確認しておきましょう.
arclengthprime[evolute[cardioid[1]]][Pi]
これで,カージオイドの縮閉線は t=0 (縮閉線にある1つのカスプに対応)と t=Pi で特異点を持つことが分かりました.
●4.3 カージオイドはリマソンの特別な場合(今の場合,リマソンのバラメータ {a,b}={0.5, 1} に対応)ですから, 今度はリマソンを考えてみましょう.まず,リマソンのパラメータ a の値を 0.5 (カージオイドの場合に対応)よりも大きく(例えば 1 に)してみましょう.
ParametricPlot[
Evaluate[{ limacon[1,1][t], evolute[limacon[1,1]][t]} ],
{t,0,2Pi},AspectRatio->Automatic];
今度は,もとの曲線(リマソン)にはカスプは現れません.その代わりに2重点が1個現れています. 縮閉線のほうはどうでしょうか.カスプが2つありますね.曲率のグラフで確かめてみましょう.
Plot[kappa2[limacon[1,1]][t], {t,0,2 Pi}]
曲率が2つの極値を持っていることが分かりますね.ここでも極小値の値は正です.
●4.4 次にリマソンのパラメータ a を 0.5 よりも小さく,例えば 0.3 に動かしてみましょう.
ParametricPlot[
Evaluate[{ limacon[0.3,1][t], evolute[limacon[0.4,1]][t]} ],
{t,0,2Pi},AspectRatio->Automatic];
今度は,リマソンにはカスプも2重点なく,リンゴの断面のような形が現れます. 縮閉線はというと,2つの連結成分が現れていますね.左側の曲線にはカスプが一つ,右側の曲線にはカスプが3つあり(合計で4つのカスプ!),各々の曲線が2つの直線に漸近している様子が観察されます. 何も指示しないと,Mathematica では自動的に(勝手に推測して)漸近線を描きます(しばしば不適当な漸近線を描くの注意が必要).曲率のグラフで確認すると,
Plot[kappa2[limacon[0.3,1]][t], {t,0,2 Pi}]
t=Pi 付近がよくわかりませんね.もっと詳しくみてみましょう.
Plot[kappa2[limacon[0.3,1]][t], {t,Pi - 0.2, Pi + 0.2}]
なるほど,t=Pi あたりで極小値になっています.ここで極小値は負の値になっていることに注意すれば,
グラフの様子から,曲率の値が0になるのは2点あるのが分かります.
一般に,曲率の値が0となる点をその平面曲線の変曲点と呼びます
このリマソンは,2つの変曲点を持っていることになります.
(注)曲率がその点の前後で符号が変わるような点のことを変曲点と呼ぶ流儀もありますが,ここでは上記の定義を使います.
曲率半径は曲率の逆数ですから,動点が変曲点に限りなく近づけば,対応する曲率中心は無限遠に飛んでいってしまいます.
この際,曲率中心は,変曲点での曲線の接線に対して垂直な直線に漸近します.
これが,ParametricPlot の描いた図に現れた2つの漸近線です.
●4.5 この辺りの事情がよく分かるように,変曲点の様子を3次関数 y= x^3 のグラフで表される平面曲線で観察してみましょう.この例では原点が変曲点です.縮閉線は, t が正のほうから0に近づくにつれ,y-軸に漸近していきます.
ParametricPlot[
Evaluate[{ curve3[1,0,0,0][t], evolute[curve3[1,0,0,0]][t]} ],
{t,-1.9, 2},AspectRatio->Automatic];
曲率のグラフは,
Plot[kappa2[curve3[1,0,0,0]][t], {t, -2, 2}]
確かに,曲率が 0 となる点がひとつだけあります.ちなみに極値は2つあって,縮閉線に2つのカスプがあることに対応しています.
変曲点であって頂点ではないものを,通常変曲点と呼びます.先に観察したような, limacon[0.3,1]][t]に現れる2つの変曲点やcurve3[1,0,0,0][t]の変曲点は,通常変曲点です. 変曲点であってしかも頂点となるものを,退化した変曲点と呼びます.
○ k 次関数 y =x^k (k > 3) のグラフが表す平面曲線は原点が退化した変曲点になる.曲率のグラフでそれを見てみよう.
curve3[t_]:={t, t^3};
curve4[t_]:={t, t^4};
Plot[ kappa2[curve4][t], {t,-0.5, 0.5}]
Plot[Evaluate[{ kappa2[curve4][t], kappa2[curve4][t]}, {t,-0.5, 0.5}]
●4.6 リマソンに戻りましょう.パラメータ a の値を 0.3 よりもさらに小さくしてみましょう.
ParametricPlot[
Evaluate[{ limacon[0.2,1][t], evolute[limacon[0.2,1]][t]} ],
{t,0,2Pi},AspectRatio->Automatic];
Plot[kappa2[limacon[0.2,1]][t], {t,0,2 Pi}]
今度は漸近線がありません.実際,曲率のグラフを見れば,曲率は常に正の値を取り,値が0となる点がないので変曲点はないのです.縮閉線は4つのカスプを持った星型の閉じた曲線として現れています. はじめにやった楕円のときと似たような縮閉線の形ですね.
パラメータ a=0.3 のときは,縮閉線は2つの連結成分を持ち2つの漸近線が現れていますが, パラメータ a=0.2 では,縮閉線は1つの閉じた曲線になっています. a=0.3 から a=0.2 に動く間になにが起こったのでしょう?
○ パラメータ a の値を小刻みに小さくして(例えば a=0.29, 0.28, ... として),リマソンと縮閉線がどのように変化するか, 観察してみなさい.
○ 変曲点(曲率の値が 0 となる点)が1つのみとなるようなパラメータ a の値を決定しなさい. さらに,この変曲点は退化していることを示しなさい. (曲率の最小値をパラメータ a で表して,「最小値= 0 」を解く.) このとき,頂点の個数は,やはり4個であることを確かめなさい.
●4.8 ここで,リマソンの形とその縮閉線の形,および曲率の極値に関して,パラメータ a の値を動かしたときにどのように変化するか,まとめてみよう.
| リマソン | リマソンの縮閉線 | リマソンの曲率 | |
| a > 0.5, b=1 | 2重点1つ,特異点なし,変曲点なし | 特異点が2つ(カスプ2つ) | 極大点1,極小点1(頂点は2個) |
| a=0.5, b=1 | 2重点なし,特異点1つ,変曲点なし | 特異点が2つ(カスプ1つと原点のところに1つ) | 極小点1つ(頂点は1個),t=Pi で定義できない(発散する) |
| a=0.3, b=1 | 2重点なし,特異点なし,通常変曲点2つ | 漸近線が2つ.特異点は4つ(カスプ4つ) | 極大点2,極小点2(頂点は4個) |
| a=??, b=1 | 2重点なし,特異点なし,退化した変曲点1つ | 漸近線が1つ.特異点が3つ(カスプ3つ)* | 極大点2,極小点2(頂点は4個) |
| a=0.2, b=1 | 2重点なし,特異点なし,変曲点なし | 特異点が4つ(カスプ4つ) | 極大点2,極小点2(頂点は4個) |
(*)退化した変曲点をもつリマソンも頂点は4個ある---- 縮閉線に特異点(カスプ)に対応する頂点3つと,退化した変曲点の分1つ,である. この場合,退化した変曲点に対応して,縮閉線は「無限遠に特異点(カスプ)を持つ」.
●4.9 この節の最後に,4頂点定理と呼ばれる,たいへん美しい古典的な定理を紹介しましょう.
くだけて言えば,この平面曲線上を車や自転車で進もうとするときに
ハンドルを切り返す場所が4地点以上ある,と主張しているのです.
自己交叉がなく特異点をもたない閉じた平面曲線の特別な場合として,曲線の内部の領域が凸になっているような曲線を卵形線といいます.卵形線の場合に対する4頂点定理の証明は易しく,大抵の教科書(初等的な微分幾何の教科書)に1ページほどのものが載っているので参照すること.
閉じた曲線ですから,曲率は円周上の関数(もしくは周期 2 Pi の関数)であり,
極値は少なくとも2つ(最大点・最小点)は存在するわけですが,
曲線が自己交叉がなく特異点をもたないならば,この他にさらに2つ以上の極値が必ず存在する,と言っています.
楕円やリマソン( a < 0.5, b=1 の場合---上表の下3行)は,たしかに4つの頂点を有しています.
一方,リマソン(a が 0.5 以上,b=1 の場合---上表の上2行)に対しては,自己交叉や特異点がある為,この定理は適用できません.
では,自己交叉や特異点がある場合,どのように定理の主張は変更されるべきだろう??
これは頂点の個数に関する定理であるが,変曲点に関する公式はないのだろうか??