コンピュータ

ローレンツ方程式

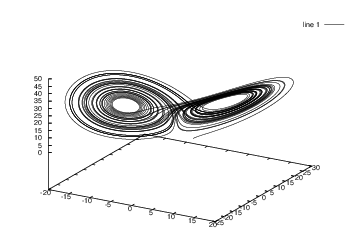
ローレンツ方程式は気象変動をモデル化した常微分方程式系であり、カオス研究の端緒を開いたものである。異なる初期値に対して軌道が不規則に解離することから長期予報の不安定性を示すものであるとされる。

\[\frac{dx}{dt} = a (x-y)\] \[\frac{dy}{dt} = -xz -y +b x\] \[\frac{dz}{dt} = xy -c z\]

ベクトル場は適切な領域内ではリプシッツ連続であり、解の一意性は満たされる。従って、込み入った軌道であっても交差しているわけではない。

三次元の微分方程式系であるから、必ずしも極限周期軌道を持つわけではない。有界な解が周期的でも定常解でもないという

a=-10, c=8/3, 24.74 > b > 145であれば、二枚の葉を持つ周期的ではない有限領域内の極限軌道が得られる。プログラム例を示す。

clear;

global a;
global b;
global c;
a=-10;
b=28;
c=8/3;

# ベクトル場の定義
function y=f(x,t)
     global a;
     global b;
     global c;
     y(1)=
     y(2)=
     y(3)=
endfunction

# 時間刻みと初期値の定義
t=linspace(0,50,10000);
x=[3,3,3];

# 数値解を得る前の時間を取得
t1=time();

# 数値解を得る
y=lsode("f", x, t);

# 数値解を得た後の時間を取得
t2=time();

# 経過時間を見る
abs(t2 - t1)

plot(y)

xx=y([1:8000],1);
yy=y([1:8000],2);
zz=y([1:8000],3);

sleep(5);

plot3(xx,yy,zz);

このプログラムでは、実行時間を計測して出力している。プログラムのどの部分が実行時間を消費しているかを知ることは速度の改善においては重要な要素である。

t1=time();で数値解を得る前の時刻を取得し、t2=time();で実行後の時刻を取得、abs(t2-t1)で時刻の差、すなわち経過時間を出力する。