コンピュータ

大域変数と局所変数

変数には有効範囲が存在する。定義した関数内で使う変数はその関数内でのみ有効である。これを局所変数と呼ぶ。関数をこえて同じ変数を利用するには、大域変数として宣言する。octaveではglobal a;として宣言する。

vdp方程式

Van der Pole方程式は次で決まる微分方程式である。パラメータ$a$によって必ず極限周期軌道を持つものとして有名である。\[\frac{du}{dt}(t) = v(t)\] \[\frac{dv}{dt}(t) = a(1-u(t)^2)v(t)-u(t)\]

プログラムは次のようになる。vdp.mとしよう。

# ベクトル場を定義する
global a=1.0;  # パラメータを大域変数として宣言

function y=f(x, t)
     # f の定義の中でa は大域変数として使用する
     global a; 
     y(1)=x(2);
     y(2)=a*(______)*x(2)-x(1);
endfunction

# 時間幅と時間刻みを決める
# t=[0:.1:50]; でもよいが、linspace 関数を使ってみる。
# linspace(x_start, x_end, N) として
# 閉区間 [x_start, x_end] をN分割した配列を返す。
t=linspace(0,50,1000);

# 初期値は ( x(1), x(2) )=( 3, 3 ) とする
x=[3,3];

# lsode 関数を使って配列 y に結果を代入する。
# y のサイズは t のサイズに等しい。
y=lsode("f", x, t);

plot( y );

# 初期値を変えてみる。
x1=[-2,1];

y1=lsode("f", x1, t);
plot( y1 );

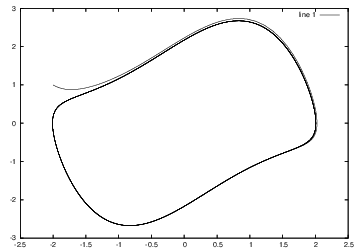
横軸にu(t),縦軸にv(t)を表示すると下図のような数値解を得る。ベクトル場を考えると定性的に妥当なものだと思われる。

プログラムの通りに実行すると横軸にt,縦軸にu(t), v(t)を表示する。妥当性は図と比較してわかるはずである。

パラメータaを大域変数と定義して変化させながら解を描画するプログラムを示す。これをvdp-2.mとしよう。

# vdp.m を読み込んだ後に実行する。
for a=[1.0:0.1:3]  # aを変えながら、
  y=lsode("f",x,t);
  plot(y); # y(1)をx座標、y(2)をy座標としてプロット
endfor