自励系の常微分方程式\[ \frac{dx}{dt}=f(x) \]を考える。$f$がリプシッツ連続であれば初期値問題の解は一意に定まる。初期値$x(0)=x_0$を与えた時の解$x(t)$から、$h>0$を固定して数列$x_n=x(nh)$を定める。この$\{x_n\}$は$x(t)$を$h$刻みで観測するものと考えられるが、$\{x_n\}$を数値的に近似して求めることで、解析的には解けない場合も解の挙動を調べることができる。ここではもっとも単純な差分法(Euler法)によるプログラムを作成する。
微分の定義にもどる。\[ \frac{dx}{dt}=\lim_{h\to 0}\frac{x(t+h)-x(t)}{h} \]右辺の極限をとらず、$h$が十分小さいとしてそのまま置き換えれば\[ \frac{x(t+h)-x(t)}{h}=f(x(t)) \]となる。$t=nh$と置いて整理し、$x_n=x(nh)$とすれば\[ x_{n+1}=x_n+f(x_n) h \]となる、この漸化式から定まる数列$\{x_n\}$を順次計算する。これをEuler法と呼ぶ。
プログラムでは関数fと初期値を決めなければならないので、ここでは$f(x)=2x$とする。
clear;
Max=100; # Max という定数を 100 と定義
dt=0.1; # 刻み幅
x=[1:Max];
function y=f( x )
y = 2.0*x;
endfunction
for n=[1:Max]
x(n+1)=x(n)+______;
endfor
plot( x );
差分法は単純なだけ誤差も大きくなる。誤差を小さくとどめる数値解法として、ルンゲクッタ法がある。
ルンゲクッタ法は、微分方程式\[\frac{dx}{dt}=f(x)\]の誤差を系統的に縮める方法である。
\[x(t+h)=x(t)+\phi h \]と置き、$\phi=f(x)$であればEuler法である。これを1次のルンゲクッタ法と呼ぶ。誤差は$h$の一次で累積する。
$\phi=w_1 k_1+w_2 k_2$, $k_1=f(x)$, $k_2=f(x+hk_1)$, $w_1=w_2=1/2$と置いた場合、誤差は$h^2$程度となる。これを修正Euler法、2次のルンゲクッタ法と呼ぶ。誤差評価は$x(t+h)$の展開と$\phi$を$h$の一次まで比較することで示せる。同様に$h$の$n$次の項まで比較することで$h^{n+1}$程度の誤差で数値解を与えるアルゴリズムを得る。これを$n$次のルンゲクッタ法と呼ぶ。
通常、単にルンゲクッタ法といえば4次のルンゲクッタ法である。
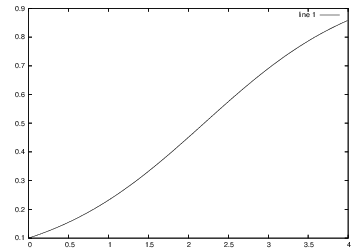
ここでは\[ \frac{dx}{dt}=x(1-x)\]のルンゲクッタ法による例をあげよう。
Max=400;
dt=0.01;
x=[1:Max];
x(1)=0.1;
function y=f( x )
y = x*(1-x);
endfunction
k=[1:4];
for i=[1:Max-1]
k(1)=dt*f(x(i));
k(2)=dt*f(x(i)+k(1)/2);
k(3)=dt*f(x(i)+k(2)/2);
k(4)=dt*f(x(i)+k(3));
x(i+1)=x(i)+(k(1)+2*k(2)+2*k(3)+k(4))/6;
endfor
plot(x);

octave:1> source "runge.m" # ファイル名をrunge.mとして例を実行 octave:2> t=[0:dt:Max*dt-dt]; # 時間刻みの設定 octave:3> function y=g(x) # 解析解をgと定義 > y=0.1*exp(x)/(1-0.1+0.1*exp(x)); > endfunction octave:4> for k=[1:400] # 配列 y へ時間刻みごとに解析解 > y(k)=g(t(k)); # の値を代入 > endfor octave:5> plot(t,x,t,y) octave:6> for k=[1:400] # 配列 z へ時間刻みごとに誤差 > z(k)=abs(x(k)-y(k)); # の値を代入 > endfor octave:7> plot(t,z)